期权作为非线性工具，其影响因素除了线性工具的标的价格，还包括剩余到期时间、波动率、资金成本等非线性因素。上一篇文章我们简单介绍了期权价格的影响因素，本篇开始我们将单独对期权价格每个影响因素的敏感性进行分析。
期权价格对影响因素的敏感性在数学上的表达是期权价格对该影响因素的一阶或多阶导数，我们称之为期权的风险参数，或者希腊字母。风险参数的控制是期权交易员面对的核心问题，期权交易本质上是通过控制各个风险参数的敞口来获得预期的风险暴露，进而获得相应的风险回报。下面这个公式展示的是期权价格变化的分解，即期权交易的获利来源。
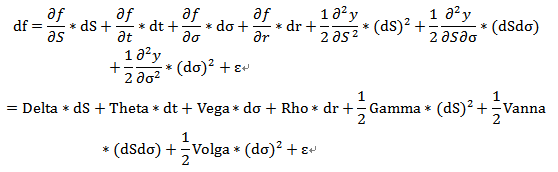
Delta的表达式
这篇文章我们首先介绍期权价格关于标的价格方向的一阶敏感性即Delta，这是投资者最熟悉的风险参数。从式子中可以看到Delta的收益来源是标的价格方向的变化，当标的价格变动dS时，期权价格变动Delta个单位。现货（如股票、ETF、股指等）的Delta是1，当你买入持有一份现货时，其涨跌幅与标的一致。
那么期权Delta的表达式是怎样的？这里我们需要借助有解析的模型才能获得具体的表达式，业界目前常用的模型为BSM模型。
在BSM世界里，普通欧式期权的理论价格公式如下：
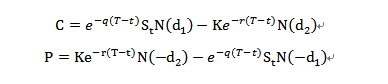
其中
上面的公式里，q是股息率，
是t时刻标的价格。Delta是定价公式对S的一阶偏导，具体的公式如下：
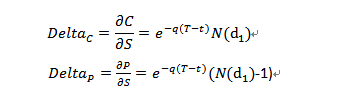
如何理解Delta
Delta在期权中有不同的理解角度，不同的角度提供了不同的思路，我们下面对其进行简要介绍。
①变化率，即标的资产价格变动时，期权价格对应的变化。假设市场中其他条件不变，那么认购期权价格的变动方向应该与标的市场相同，认沽期权则正好相反。如某个认购期权合约的Delta为0.25，那么该期权价值变化速度应该是标的资产价格变化率的25%，即如果标的资产价格上涨（下跌）1.0，那么期权价格将上涨（下跌）0.25。认购期权的Delta值为0到1之间（图1），认沽期权的Delta值为-1到0之间（图2），两者均呈S型。
图1 ：认购期权Delta
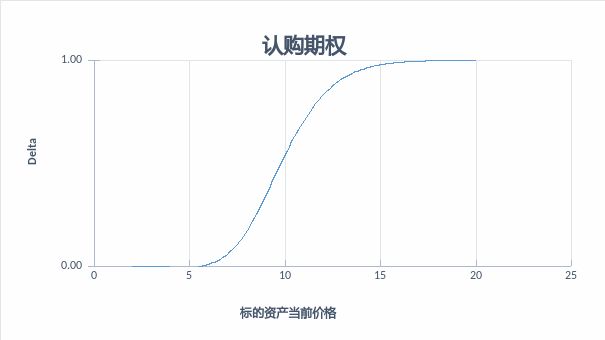图：富荣基金量化组图2 ：认沽期权的Delta
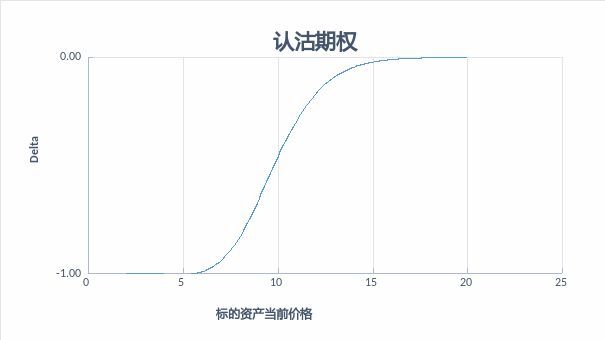图：富荣基金量化组②对冲比率。实践中常见的中性策略通常指的就是Delta中性，例如买入标的同时卖出相同敞口的期货即是一种Delta中性策略。期权构建的Delta中性策略同理，假设标的资产的Delta值为1，认购期权的Delta值为0.5，那么适当的对冲比率就是2，也就是说每买入（卖出）2份期权就应该卖出（买入）1份标的合约来建立Delta中性策略。
③概率（这是一个近似的结果，只是有助于理解）。忽略Delta的符号，Delta是期权到期变为实值期权的概率。例如一个合约的Delta值为0.25，我们可以理解为该合约到期日有25%的概率变为实值期权。读者如果感兴趣的话，可以发现在BSM框架下，无分红的欧式期权到期变为实值的概率是
，我们这里将近似看成，存在一定误差，但是这个思路有助于我们去理解。此外，不同于BSM世界，实际市场中存在很多因素可能会扭曲这个表达式的有效性，因此我们也需要注意到这个思路的局限性。Delta的影响因素
在对Delta有个简单的印象之后，我们想要分析Delta在不同的环境下是如何变动的？我们这里选取两个最重要的影响因素：剩余到期时间和波动率。
①剩余到期时间对Delta的影响。期权剩余到期时间越大，每个合约的可能性越多，我们不能确定这个合约在到期时是实值、虚值还是平值，从而我们只能给出一个平均值的判断（即Delta等于0.5，这是最大限度的不确定性）。期权的剩余到期时间越长，Delta绝对值会越趋向于0.5，然后随着到期日的临近Delta会趋近于确定，成为实值概率大的Delta绝对值趋向于1，成为虚值概率大的Delta绝对值趋向于0，仍然不太明确的Delta绝对值依然在0.5附近。（图3、4）
图3：认购期权Delta与剩余期限的关系
图：富荣基金量化组图4 ：认沽期权Delta与剩余期限的关系
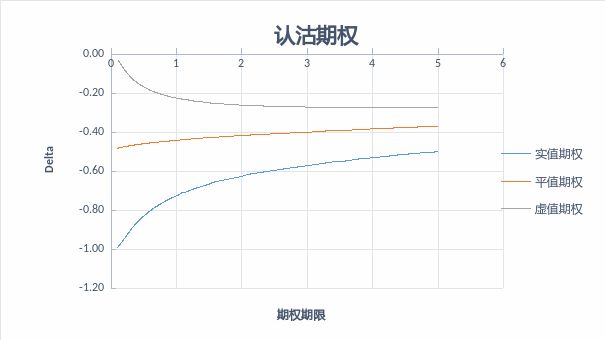图：富荣基金量化组②波动率对Delta的影响。标的价格的变化对Delta的影响比较直观，但是波动率对Delta的影响通常会让人忽视，其中一个原因是波动率对Delta的影响是脉冲式的。
在波动率发生较大变化情况下（驱动隐含波动率上升的原因可能是实际波动率上升的，也可能是交易员对未来预期的转变），Delta也会发生较大的变化。波动率上升时，投资者预期未来标的的波动幅度将加大，这也就意味着不同合约在未来的差异性将降低，到期成为实值的概率将降低，从而虚值期权的Delta会上升，实值期权的Delta会下降，都向代表不确定性的0.5靠拢（图5、6）。
图5 ：认购期权波动率和Delta的关系
图：富荣基金量化组图6：认沽期权波动率和Delta的关系
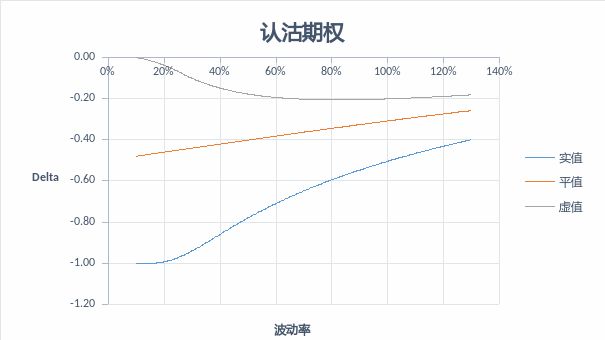图：富荣基金量化组风险提示：1、本报告中的信息均来源于我们认为可靠的已公开资料和合作客户的研究成果，但本公司及研究人员对这些信息的准确性和完整性不作任何保证，也不保证本报告所包含的信息或建议在本报告发出后不会发生任何变更，且本报告仅反映发布时的资料、观点和预测，可能在随后会作出调整。2、本报告中的资料、观点和预测等仅供参考，在任何时候均不构成对任何人的个人推荐。市场有风险，投资需谨慎。
